データ分析において、ある仮説が正しいかどうかを検証することは重要です。その際に用いられる統計手法が 仮説検定(Hypothesis Testing) です。本記事では、仮説検定の基本概念を理解し、Excelを使って簡単にp値を求め、有意差を確認する方法を解説します。
1. 仮説検定とは?
仮説検定とは、データに基づいてある主張(仮説)が正しいかどうかを統計的に検証する方法です。
仮説検定の基本概念
| 用語 | 説明 |
|---|---|
| 帰無仮説(H₀) | 検定で否定しようとする仮説(例:「新しい薬に効果はない」) |
| 対立仮説(H₁) | 帰無仮説が否定された場合に採択される仮説(例:「新しい薬には効果がある」) |
| p値 | 仮説が偶然に起こる確率(小さいほど帰無仮説を棄却しやすい) |
| 有意水準(α) | 統計的に有意と判断する基準(一般的には 5% = 0.05) |
例えば、「新しいマーケティング施策で売上が増加するか」を検証する場合、
- H₀(帰無仮説):マーケティング施策の効果はない
- H₁(対立仮説):マーケティング施策の効果がある となります。
2. Excelで仮説検定を実施する方法
Excelでは、仮説検定を行うために T.TEST関数 や データ分析ツール を活用できます。
T.TEST関数を使う方法
Excelの T.TEST 関数を使って、p値を求めることができます。
T.TEST関数の構文
=T.TEST(配列1, 配列2, 検定の種類, 検定方法)T.TEST関数の例
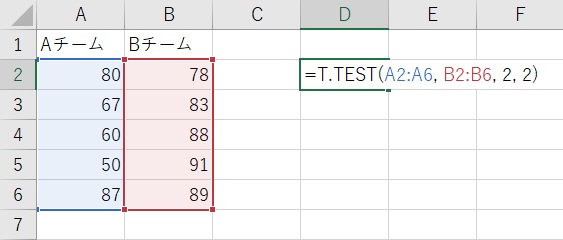
=T.TEST(A2:A6, B2:B6, 2, 2)この場合、
2(第三引数:検定の種類):1=片側検定, 2=両側検定(通常は2)2(第四引数:検定方法):1=等分散, 2=不等分散(通常は2)
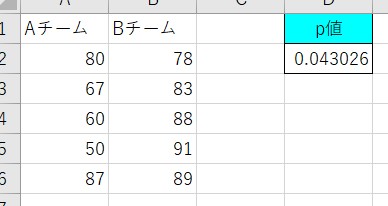
p値が 0.05未満 なら、「統計的に有意な差がある」と判断します。
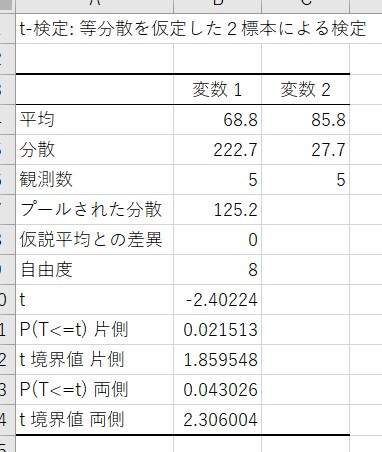
今回はp値が「0.043026」のため、「統計的に有意な差がある」と判断します。
データ分析ツールを使う方法
Excelの「データ分析」ツールを使えば、詳細な仮説検定の結果を出力できます。
手順
- 「データ」タブ → 「データ分析」をクリック

- 「t検定(一対・等分散・分散が等しくない)」のいずれかを選択し、「OK」
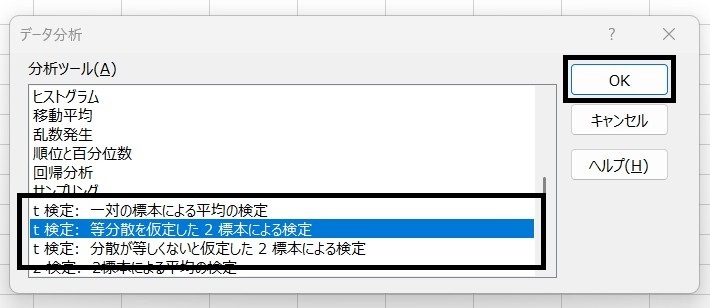
- データ範囲(A列とB列)を選択
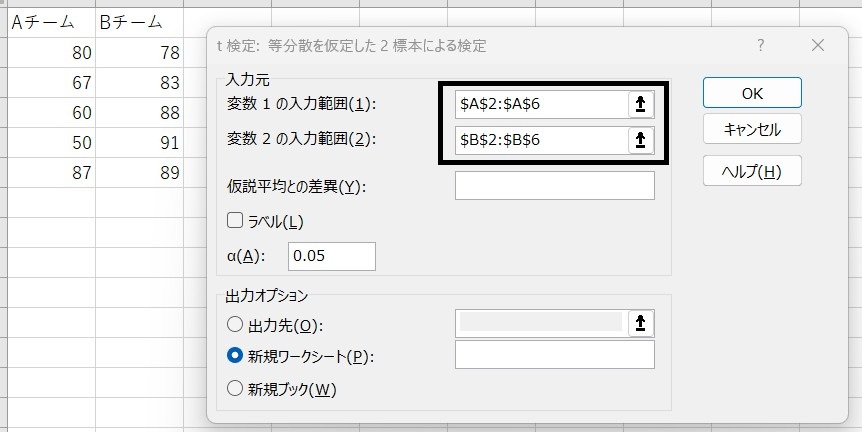
- 「出力範囲」を指定し、「OK」をクリック
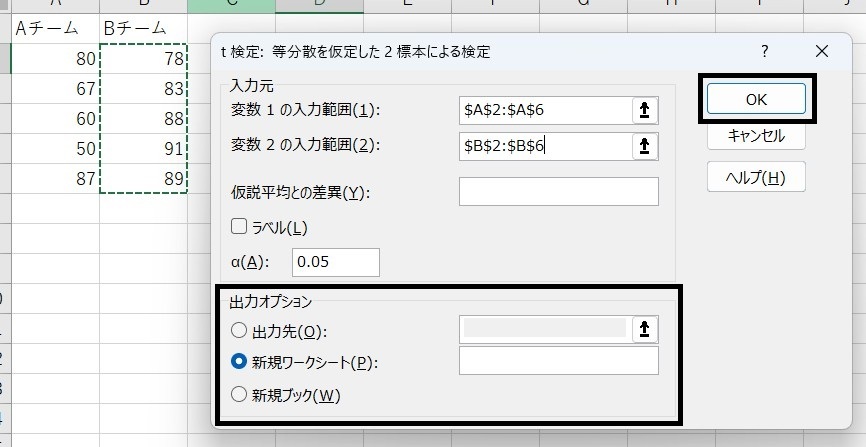
この方法では、平均値、t値、p値、自由度などの詳細な分析結果が得られます。
3. 仮説検定の活用例
(1) 新商品の販売効果検証
- 例:「プロモーション実施前と実施後の売上に差があるか」を検証する。
- p値 < 0.05 なら、プロモーションに有意な効果があると判断できる。
(2) 医薬品の効果分析
- 例:「新薬を服用した患者とプラセボを服用した患者の症状改善率の比較」
- p値 < 0.05 なら、新薬に統計的な効果があると考えられる。
(3) A/Bテストの結果分析
- 例:「新しいウェブページのデザインと旧デザインでコンバージョン率に差があるか」
- p値 < 0.05 なら、新デザインの方が有効といえる。
4. 仮説検定の注意点
(1) p値の解釈を誤らない
- p値が小さい=効果が大きいわけではない
- p値が大きい=まったく差がないわけではない
(2) サンプルサイズの影響
- サンプルサイズが小さいと、統計的な有意差が見えにくい。
- 適切なサンプルサイズを確保することが重要です。
(3) 多重検定の問題
- 複数の検定を行うと、偶然による有意差が出る可能性が高まる。
- 必要に応じてボンフェローニ補正などの手法を考慮する。
まとめ
- 仮説検定は、2つのグループ間の統計的な差を検証する手法です。
- ExcelのT.TEST関数やデータ分析ツールを使えば、簡単にp値を求められる。
- p値が0.05未満なら、統計的に有意な差があると判断できる。
- データの解釈や検定の選択に注意しながら、適切に活用することが重要です。
p値によって、統計的に有意な差があると判断できますが、毎回、0.05未満か違うのかでドキドキしたりしてました(笑)
仮説検定を活用して、データに基づいた意思決定を行いましょう!
関連記事(t検定とは?Excelで2つのグループの平均を比較する方法)がありますので、ご覧ください。

コメント