データ分析において、2つのグループの平均値に違いがあるかを検証することは重要です。その際に用いられる統計手法の一つが t検定（t-test） です。本記事では、t検定の基本を理解し、Excelを使って簡単に実施する方法を解説します。
1. t検定とは？
t検定 は、2つのグループの平均値に統計的な差があるかを検証するための手法です。
t検定の種類
| 種類 | 使う場面 |
|---|---|
| 対応のないt検定（独立サンプルt検定） | 2つの独立したグループの平均値を比較する（例：A社とB社の売上） |
| 対応のあるt検定（対応のあるサンプルt検定） | 同じ対象の前後データを比較する（例：ダイエット前後の体重） |
| 等分散・異分散の違い | 2つのグループの分散が等しいかどうかで使い分ける |
例えば、「広告施策Aを実施した店舗と実施しなかった店舗で売上に差があるか」を調べる場合、独立サンプルt検定を使います。
2. Excelでt検定を実施する方法
Excelには、t検定を簡単に行う T.TEST関数 と データ分析ツール があります。
T.TEST関数を使う方法
Excelの T.TEST 関数を使うと、2つのグループのデータからp値を求めることができます。
T.TEST関数の構文
=T.TEST(配列1, 配列2, 検定の種類, 検定方法)T.TEST関数の例
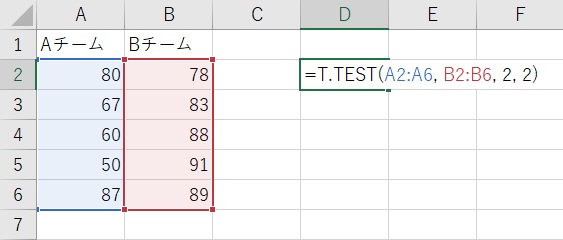
=T.TEST(A2:A6, B2:B6, 2, 2)この場合、
2（第三引数：検定の種類）：1=片側検定, 2=両側検定（通常は2）2（第四引数：検定方法）：1=等分散, 2=不等分散（通常は2）
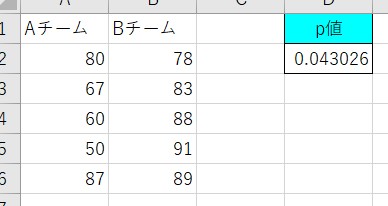
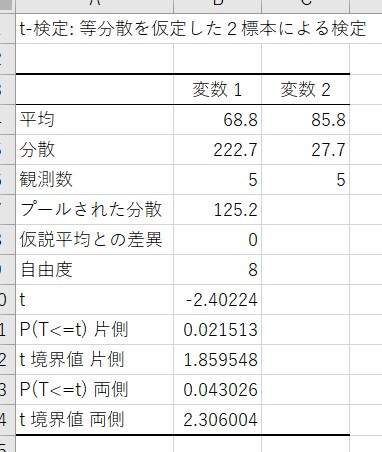
p値が 0.05未満 なら、「2つのグループに統計的に有意な差がある」と判断します。
今回はp値が「0.043026」のため、「統計的に有意な差がある」と判断します。
データ分析ツールを使う方法
Excelの「データ分析」ツールを使えば、詳細な仮説検定の結果を出力できます。
手順
- 「データ」タブ → 「データ分析」をクリック
- 「t検定（一対・等分散・分散が等しくない）」のいずれかを選択し、「OK」
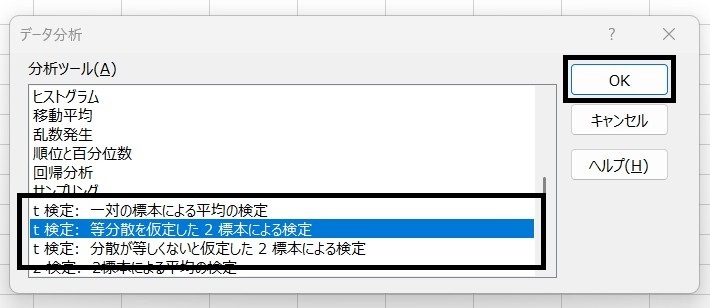
- データ範囲（A列とB列）を選択
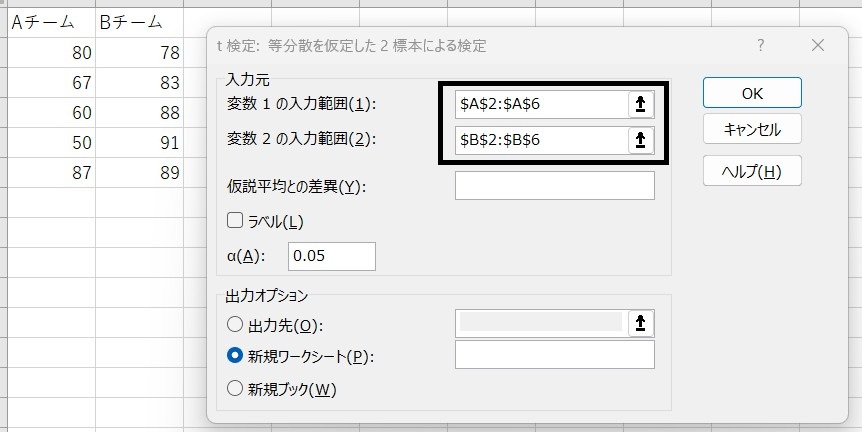
- 「出力範囲」を指定し、「OK」をクリック
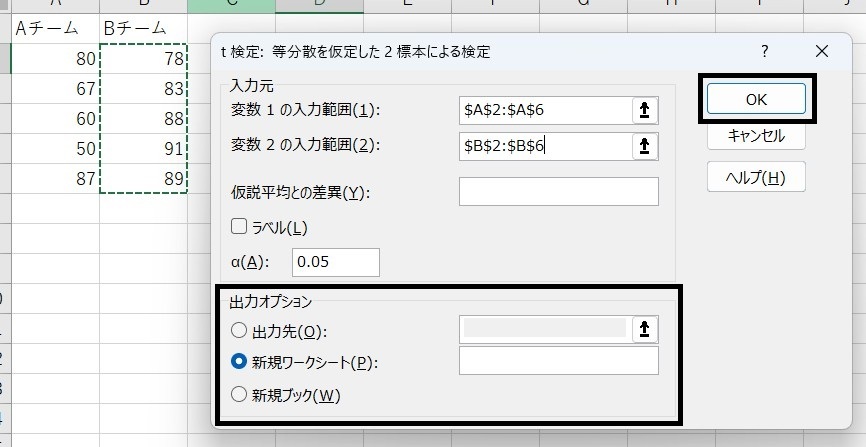
この方法では、平均値、t値、p値、自由度などの詳細な分析結果が得られます。
3. t検定の活用例
(1) 広告の効果検証
- 例：「広告Aを実施した店舗」と「広告Aを実施しなかった店舗」の売上を比較する。
- p値 < 0.05 なら、広告Aの影響が有意と判断できる。
(2) 医薬品の効果分析
- 例：「薬を飲んだ患者」と「飲まなかった患者」の血圧変化を比較する。
- p値 < 0.05 なら、薬が効果的である可能性が高い。
(3) 学習方法の比較
- 例：「新しい学習法を試した生徒」と「従来の方法の生徒」のテスト結果を比較する。
- p値 < 0.05 なら、新しい学習法の効果が有意といえる。
4. t検定の注意点
(1) 外れ値の影響
- 極端な値があると、t検定の結果が大きく変わる可能性があります。
- データの分布を事前に確認し、外れ値が影響しないかチェックする。
(2) データ数が少ないと信頼性が低くなる
- データ数が少ないと、統計的に意味のある結果を得るのが難しくなる。
- できるだけ十分なデータを確保する。
(3) 検定の選択を間違えない
- 対応あり or 対応なし、等分散 or 異分散 を正しく設定しないと、誤った結論を導く可能性がある。
まとめ
- t検定は2つのグループの平均値の差を検証する統計手法です。
- ExcelのT.TEST関数やデータ分析ツールを使えば、簡単にt検定を実施できる。
- p値が0.05未満なら、2つのグループに統計的な差があると判断できる。
- 外れ値やデータ数に注意しながら、適切に活用することが重要です。
t検定を行う前にF検定を行ったりする場合があります。いろいろな検定が存在しますが、データに即した検定を扱えるようにしましょう。
t検定を活用して、データに基づいた意思決定を行いましょう！
コメント